Classical Mechanics Practice Problems (Part I)

Review

• 3D vector representation of space: $$\mathbf{r}=x \hat{\mathbf{x}}+y \hat{\mathbf{y}}+z \hat{\mathbf{z}}=(x, y, z)$$
  • Sum: $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$ and $\mathbf{s}=\left(s_{1}, s_{2}, s_{3}\right)$ $$\mathbf{r}+\mathbf{s}=\left(r_{1}+s_{1}, r_{2}+s_{2}, r_{3}+s_{3}\right)$$
  • Scalar multiplication: $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$ $$c \mathbf{r}=\left(c r_{1}, c r_{2}, c r_{3}\right)$$
  • Dot product (scalar product): $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$ and $\mathbf{s}=\left(s_{1}, s_{2}, s_{3}\right)$ $$\mathbf{r} \cdot \mathbf{s}=|\mathbf{r}| |\mathbf{s}| \cos \theta=r_{1} s_{1}+r_{2} s_{2}+r_{3} s_{3}=\sum_{n=1}^{3} r_{n} s_{n}$$
  • Norm (length): $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$ $$r=|\mathbf{r}|=\sqrt{\mathbf{r} \cdot \mathbf{r}}=\sqrt{r_{1}^{2}+r_{2}^{2}+r_{3}^{2}}$$
  • Vector product (cross product): $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$ and $\mathbf{s}=\left(s_{1}, s_{2}, s_{3}\right)$ $$\mathbf{r} \times \mathbf{s}=\operatorname{det}\left[\begin{array}{ccc}\hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \ r_{x} & r_{y} & r_{z} \ s_{x} & s_{y} & s_{z}\end{array}\right]=(r_{y} s_{z}-r_{z} s_{y}, r_{z} s_{x}-r_{x} s_{z}, r_{x} s_{y}-r_{y} s_{x})$$
    If the angle between them is $\theta$, we also have $$|\mathbf{r} \times \mathbf{s}|=|\mathbf{r}| |\mathbf{s}| \sin \theta.$$
• Velocity: The velocity of an object is the rate of change of its position with respect to a frame of reference, and is a function of time. $$\mathbf{v}=\frac{d \mathbf{r}}{d t}=v_{x} \hat{\mathbf{x}}+v_{y} \hat{\mathbf{y}}+v_{z} \hat{\mathbf{z}}=\frac{d x}{d t} \hat{\mathbf{x}}+\frac{d y}{d t} \hat{\mathbf{y}}+\frac{d z}{d t} \hat{\mathbf{z}}$$
• Acceleration: Acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities. $$\mathbf{a}=\frac{d \mathbf{v}}{d t}=a_{x} \hat{\mathbf{x}}+a_{y} \hat{\mathbf{y}}+a_{z} \hat{\mathbf{z}}=\frac{d^2 x}{d t^2} \hat{\mathbf{x}}+\frac{d^2 y}{d t^2} \hat{\mathbf{y}}+\frac{d^2 z}{d t^2} \hat{\mathbf{z}}$$
• Time: Time is the continued sequence of existence and events that occurs in an apparently irreversible succession from the past, through the present, into the future: $t$.
• Reference Frame: In physics, a frame of reference (or reference frame) is an abstract coordinate system with an origin, orientation, and scale specified by a set of reference points―geometric points
  • Inertial Frame $\mathcal{S}$: In classical physics and special relativity, an inertial frame of reference is a frame of reference that is not undergoing acceleration.
    • It is a frame of reference in which Newton’s first law of motion holds.
    • The physics of a system in an inertial frame have no causes external to the system.
    • In classical physics and special relativity, the physics of a system vary depending on the acceleration of that frame with respect to an inertial frame
• Degree of freedom: Degrees of Freedom refers to the number of independent variables or parameters of a system.
• Mass: Mass is the quantity of matter in a physical body. It is also a measure of the body’s inertia.
• Force: In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity.
• Newton’s laws: Newton’s laws of motion are three laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it.
  • Newton’s 1st law (the Law of Inertia): In the absence of forces, a particle moves with constant velocity $\mathbf{v}$.
  • Newton’s 2nd law: For any particle of mass $m$, the net force $\mathbf{F}$ on the particle is always equal to the mass $m$ times the particle’s acceleration: $$\mathrm{F}=m \mathrm{a}.$$
    • Momentum: $\mathbf{p}=m \mathbf{v}$ $$\dot{\mathbf{p}}=m \dot{\mathbf{v}}=m \mathbf{a}$$ $$\mathbf{F}=\dot{\mathbf{p}}$$
  • Newton’s 3rd law: If object 1 exerts a force $\mathbf{F}{21}$ on object 2 , then object 2 always exerts a reaction force $\mathbf{F}{12}$ on object 1 given by $$\mathbf{F}{12}=-\mathbf{F}{21}.$$
• Solve differential equations: For instance, $\ddot{x}(t)=\frac{F_{\mathrm{o}}}{m}$,
  $$
  \dot{x}(t)=\int \ddot{x}(t) d t=v_{\mathrm{o}}+\frac{F_{\mathrm{o}}}{m} t
  $$
  $$
  x(t)=\int \dot{x}(t) d t=x_{\mathrm{o}}+v_{\mathrm{o}} t+\frac{F_{\mathrm{o}}}{2 m} t^{2}
  $$
• Central forces: In classical mechanics, a central force on an object is a force that is directed towards or away from a point called center of force.
  $$
  \vec{F}=\mathbf{F}(\mathbf{r})=|F(\mathbf{r})| \hat{\mathbf{r}}
  $$
• Conservation of Momentum: If the net external force $\mathbf{F}^{\mathrm{ext}}$ on an $N$-particle system is zero, the system’s total momentum $\mathbf{P}$ is constant. $$\dot{\mathbf{P}}=\sum_{\alpha} \mathbf{F}_{\alpha}^{\mathrm{ext}} \equiv \mathbf{F}^{\mathrm{ext}}$$
  • In a closed system the total momentum remains constant. This fact, known as the law of conservation of momentum, is implied by Newton’s laws of motion.
• Coordinate Frames:
  • Newton’s Second Law in Cartesian Coordinates: $$\mathbf{F}=F_{x} \hat{\mathbf{x}}+F_{y} \hat{\mathbf{y}}+F_{z} \hat{\mathbf{z}}=m \ddot{x} \hat{\mathbf{x}}+m \ddot{y} \hat{\mathbf{y}}+m \ddot{z} \hat{\mathbf{z}} .=m \ddot{\mathbf{r}}$$
  • Transfer in between Polar and Cartesian Coordinate (2D): $$\left.\begin{array}{l}x=r \cos \phi \y=r \sin \phi\end{array}\right} \longleftrightarrow\left{\begin{array}{l}r=\sqrt{x^{2}+y^{2}} \\phi=\arctan (y / x)\end{array}\right.$$
  • Newton’s Second Law in Polar Coordinates (2D): $$\mathbf{F}=F_{r} \hat{\mathbf{r}}+F_{\phi} \hat{\boldsymbol{\phi}}$$ $$\left{\begin{array}{c}F_{r}=m\left(\ddot{r}-r \dot{\phi}^{2}\right) \F_{\phi}=m(r \ddot{\phi}+2 \dot{r} \dot{\phi})\end{array}\right.$$
  • Newton’s Second Law in Cylindrical Coordinates: $$\mathbf{F}=F_{r} \hat{\mathbf{r}}+F_{\phi} \hat{\boldsymbol{\phi}}+F_{z} \hat{\boldsymbol{z}}$$$$\left{\begin{array}{l}F_{r}=m\left(\ddot{\rho}-\rho \dot{\phi}^{2}\right) \F_{\phi}=m(\rho\ddot{\phi}+2 \dot{\rho} \dot{\phi}) \F_{z}=m \ddot{z}\end{array}\right.$$

John R. Taylor — Question 1.2

Question: Two vectors are given as $\mathbf{b}=(1,2,3)$ and $\mathbf{c}=(3,2,1) .$ (Remember that these statements are just a compact way of giving you the components of the vectors.) Find $\mathbf{b}+\mathbf{c}, 5 \mathbf{b}-2 \mathbf{c}, \mathbf{b} \cdot \mathbf{c}$, and $\mathbf{b} \times \mathbf{c}$.

Answer:

• $\mathbf{b}+\mathbf{c}=(1,2,3)+(3,2,1)=(4,4,4)$
• $5 \mathbf{b}-2 \mathbf{c}=5\times(1,2,3)-2\times(3,2,1)=(5,10,15)-(6,4,2)=(-1,6,13)$
• $\mathbf{b} \cdot \mathbf{c}=1\times3+2\times2+3\times1=10$
• $\begin{align}\mathbf{b} \times \mathbf{c}&=\operatorname{det}\left[\begin{array}{ccc}\hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \ 1 & 2 & 3 \ 3 & 2 & 1\end{array}\right]\&=(2 \times 1-3 \times 2, 3 \times 3-1 \times 1, 1 \times 2-2 \times 3)\&=(2-6,9-1,2-6)\&=(-4,8,-4)\end{align}$

John R. Taylor — Question 1.3

Question: By applying Pythagoras’s theorem (the usual two-dimensional version) twice over, prove that the length $r$ of a three-dimensional vector $\mathbf{r}=(x, y, z)$ satisfies $r^{2}=x^{2}+y^{2}+z^{2}$.

Proof:

• Firstly apply the Pythagoras’s theorem on the $xy-$plane and have $r_{x y}^{2}=x^{2}+y^{2} \Rightarrow r_{x y}=\sqrt{x^{2}+y^{2}}$.
• Then apply the Pythagoras’s theorem on the plane of $r_{xy}$ and $z$, we have $r^{2}=r_{x y z}^{2}=\left(\sqrt{x^{2}+y^{2}}\right)^{2}+z^{2}=x^{2}+y^{2}+z^{2}$.
• Hence, $r^{2}=x^{2}+y^{2}+z^{2}$.

John R. Taylor — Question 1.4

Question: One of the many uses of the scalar product is to find the angle between two given vectors. Find the angle between the vectors $\mathbf{b}=(1,2,4)$ and $\mathbf{c}=(4,2,1)$ by evaluating their scalar product.

Answer: Because of $\mathbf{r} \cdot \mathbf{s}=|\mathbf{r}| |\mathbf{s}| \cos \theta$. Then we have
$$
\cos \theta=\frac{\mathbf{b} \cdot \mathbf{c}}{|\mathbf{b}| |\mathbf{c}|}
=\frac{1\times4+2\times2+4\times1}{\sqrt{1^2+2^2+4^2}\cdot\sqrt{4^2+2^2+1^2}}
=\frac{12}{21}=\frac{4}{7},
$$
hence,
$$\theta=\arccos(4/7)\approx55.15^\circ.$$

John R. Taylor — Question 1.6

Question: By evaluating their dot product, find the values of the scalar $s$ for which the two vectors $\mathbf{b}=\hat{\mathbf{x}}+s \hat{\mathbf{y}}$ and $\mathbf{c}=\hat{\mathbf{x}}-s \hat{\mathbf{y}}$ are orthogonal. (Remember that two vectors are orthogonal if and only if their dot product is zero.) Explain your answers with a sketch.

Answer: The dot product of two orthogonal vectors is zero. The condition of $\mathbf{b}$ and $\mathbf{c}$ to be orthgonal is
$$
\mathbf{b}\cdot\mathbf{c}=1\cdot1+s\cdot(-s)=1-s^2\equiv0,
$$
solve the equation $1-s^2=0$ shows us the scalar $s$ should be $s=\pm1$. Why there are to possible $s$? If we graph it on a 2d-plane, such as this:

As we can see, the orthogonal vectors are $(1,1)$ and $(1,-1)$, if $s=+1$, then $\mathbf{b}=\hat{\mathbf{x}}+\hat{\mathbf{y}}=(1,1)$ and $\mathbf{c}=\hat{\mathbf{x}}-\hat{\mathbf{y}}=(1,-1)$; else if $s=-1$, then $\mathbf{b}=\hat{\mathbf{x}}-\hat{\mathbf{y}}=(1,-1)$ and $\mathbf{c}=\hat{\mathbf{x}}+\hat{\mathbf{y}}=(1,1)$. The two vectors switches, but doesn’t matter, both makes the orthogonality exists.

John R. Taylor — Question 1.8

Question: (a) Use the definition (1.7) to prove that the scalar product is distributive, that is, $\mathbf{r} \cdot(\mathbf{u}+\mathbf{v})=\mathbf{r} \cdot \mathbf{u}+\mathbf{r} \cdot \mathbf{v}$. (b) If $\mathbf{r}$ and $\mathbf{s}$ are vectors that depend on time, prove that the product rule for differentiating products applies to $\mathbf{r} \cdot \mathbf{s}$, that is, that
$$
\frac{d}{d t}(\mathbf{r} \cdot \mathbf{s})=\mathbf{r} \cdot \frac{d \mathbf{s}}{d t}+\frac{d \mathbf{r}}{d t} \cdot \mathbf{s}.
$$

Proof of (a): The definition (1.7) tells us that, for $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$ and $\mathbf{s}=\left(s_{1}, s_{2}, s_{3}\right)$,
$$\mathbf{r} \cdot \mathbf{s}=|\mathbf{b}| |\mathbf{c}| \cos \theta=r_{1} s_{1}+r_{2} s_{2}+r_{3} s_{3}=\sum_{n=1}^{3} r_{n} s_{n}.$$
Therefore, for $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$, $\mathbf{u}=\left(u_{1}, u_{2}, u_{3}\right)$ and $\mathbf{v}=\left(v_{1}, v_{2}, v_{3}\right)$, on the one hand,
$$
\begin{align}
\mathbf{r} \cdot(\mathbf{u}+\mathbf{v})
&=\left(r_{1}, r_{2}, r_{3}\right)\cdot\left(u_{1}+v_{1}, u_{2}+v_{2}, u_{3}+v_{3}\right)\
&=r_{1}(u_{1}+v_{1})+r_{2}(u_{2}+v_{2})+r_{3}(u_{3}+v_{3}),
\end{align}
$$
on the other hand,
$$
\begin{align}
\mathbf{r} \cdot \mathbf{u}+\mathbf{r} \cdot \mathbf{v}
&=r_{1}u_{1}+r_{2}u_{2}+r_{3}u_{3}+r_{1}v_{1}+r_{2}v_{2}+r_{3}v_{3}\
&=r_{1}(u_{1}+v_{1})+r_{2}(u_{2}+v_{2})+r_{3}(u_{3}+v_{3}),
\end{align}
$$
this tells us that $\mathbf{r} \cdot(\mathbf{u}+\mathbf{v})=\mathbf{r} \cdot \mathbf{u}+\mathbf{r} \cdot \mathbf{v}$, so proved the dot product being distributive.

Proof of (b): We suppose that the $\mathbf{r}$ and $\mathbf{s}$ are vectors that depend on time, mathematically, $\mathbf{r}=\left(r_{1}(t), r_{2}(t), r_{3}(t)\right)$ and $\mathbf{s}=\left(s_{1}(t), s_{2}(t), s_{3}(t)\right)$, so
$$
\begin{align}
\frac{d}{d t}(\mathbf{r} \cdot \mathbf{s})
=&\frac{d}{d t}(r_{1}(t) s_{1}(t)+r_{2}(t) s_{2}(t)+r_{3}(t) s_{3}(t))\
=&\frac{d}{d t}r_{1}(t) s_{1}(t)+r_{1}(t) \frac{d}{d t}s_{1}(t)\
&+\frac{d}{d t}r_{2}(t) s_{2}(t)+r_{2}(t) \frac{d}{d t}s_{2}(t)\
&+\frac{d}{d t}r_{3}(t) s_{3}(t)+r_{3}(t) \frac{d}{d t}s_{3}(t)
\end{align}
$$
and
$$
\begin{align}
\mathbf{r} \cdot \frac{d \mathbf{s}}{d t}+\frac{d \mathbf{r}}{d t} \cdot \mathbf{s}
=&\left(r_{1}(t), r_{2}(t), r_{3}(t)\right)\cdot\left(\frac{d}{d t}s_{1}(t), \frac{d}{d t}s_{2}(t), \frac{d}{d t}s_{3}(t)\right)\
&+\left(\frac{d}{d t}r_{1}(t), \frac{d}{d t}r_{2}(t), \frac{d}{d t}r_{3}(t)\right)\cdot\left(s_{1}(t), s_{2}(t), s_{3}(t)\right)\
=&r_{1}(t) \frac{d}{d t}s_{1}(t)+r_{2}(t) \frac{d}{d t}s_{2}(t)+r_{3}(t) \frac{d}{d t}s_{3}(t)\
&+\frac{d}{d t}r_{1}(t) s_{1}(t)+\frac{d}{d t}r_{2}(t) s_{2}(t)+\frac{d}{d t}r_{3}(t) s_{3}(t)\
=&\frac{d}{d t}r_{1}(t) s_{1}(t)+r_{1}(t) \frac{d}{d t}s_{1}(t)\
&+\frac{d}{d t}r_{2}(t) s_{2}(t)+r_{2}(t) \frac{d}{d t}s_{2}(t)\
&+\frac{d}{d t}r_{3}(t) s_{3}(t)+r_{3}(t) \frac{d}{d t}s_{3}(t)
\end{align}
$$
this tells us that $\frac{d}{d t}(\mathbf{r} \cdot \mathbf{s})=\mathbf{r} \cdot \frac{d \mathbf{s}}{d t}+\frac{d \mathbf{r}}{d t} \cdot \mathbf{s}$, so proved the product rule of vector dot product.

John R. Taylor — Question 1.12

Question: The position of a moving particle is given as a function of time $t$ to be
$$
\mathbf{r}(t)=\hat{\mathbf{x}} b \cos (\omega t)+\hat{\mathbf{y}} c \sin (\omega t)+\hat{\mathbf{z}} v_{\mathrm{o}} t
$$
where $b, c, v_{\mathrm{o}}$ and $\omega$ are constants. Describe the particle’s orbit.

Answer: To simplify the problem, we only consider the $xy$-plane at beginning, which is
$$
\hat{\mathbf{x}} x(t)+\hat{\mathbf{y}} y(t)=\hat{\mathbf{x}} b \cos (\omega t)+\hat{\mathbf{y}} c \sin (\omega t)
$$
for that $x(t)=b \cos (\omega t)$ and $y(t)=c \sin (\omega t)$, move the $c,b$ to the left side of equation and have
$$
\frac{x(t)}{b}=\cos \omega t, \quad \frac{y(t)}{c}=\sin \omega t.
$$
Recall that $\cos^2 \omega t+\sin^2 \omega t\equiv1$, so
$$
\frac{x^2(t)}{b^2}+\frac{y^2(t)}{c^2}=1,
$$
this is clearly a what is known to be an equation of the ellipse. The semi-axis of $\hat{\mathbf{x}}$ direction is $b$, the semi-axis of $\hat{\mathbf{y}}$ direction is $c$. And this ellipse is the motion of the particle on the $xy-$plane.

Then, on the $\hat{\mathbf{z}}$ direction, we have the particle moving along $\hat{\mathbf{z}}$ direcion with a constant velocity $v_0$.

Together, the motion in the 3d Cartesian coordinate, since $xy-$plane motion gives a ellipse and $\hat{\mathbf{z}}$ direcion motion gives an uniform linear motion, is a helix of ellipse motion.

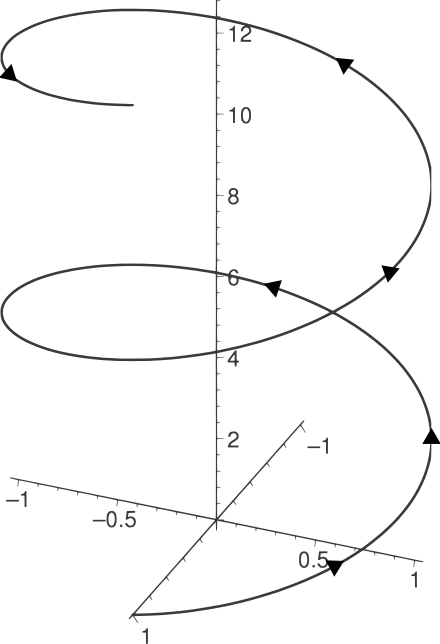
John R. Taylor — Question 1.17

Question: (a) Prove that the vector product $\mathbf{r} \times \mathbf{s}$ as defined by (1.9) is distributive; that is, that $\mathbf{r} \times(\mathbf{u}+\mathbf{v})=(\mathbf{r} \times \mathbf{u})+(\mathbf{r} \times \mathbf{v})$. (b) Prove the product rule
$$
\frac{d}{d t}(\mathbf{r} \times \mathbf{s})=\mathbf{r} \times \frac{d \mathbf{s}}{d t}+\frac{d \mathbf{r}}{d t} \times \mathbf{s}
$$
(Be careful with the order of the factors.)

Proof of (a): The definition (1.7) tells us that, for $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$ and $\mathbf{s}=\left(s_{1}, s_{2}, s_{3}\right)$,
$$|\mathbf{r} \times \mathbf{s}|=|\mathbf{b}| |\mathbf{c}| \sin \theta.$$
Therefore, for $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$, $\mathbf{u}=\left(u_{1}, u_{2}, u_{3}\right)$ and $\mathbf{v}=\left(v_{1}, v_{2}, v_{3}\right)$, on the one hand,
$$
\begin{align}
&\mathbf{r} \times(\mathbf{u}+\mathbf{v})\
=&\left[\begin{array}{ccc}\hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \ r_{1} & r_{2} & r_{3} \ u_{1}+v_{1} & u_{2}+v_{2} & u_{3}+v_{3}\end{array}\right]\
=&(r_{2} (u_{3}+v_{3})-r_{3} (u_{2}+v_{2}), r_{3} (u_{1}+v_{1})-r_{1} (u_{3}+v_{3}), r_{1} (u_{2}+v_{2})-r_{2} (u_{1}+v_{1})),
\end{align}
$$
on the other hand,
$$
\begin{align}
&\mathbf{r} \times \mathbf{u}\
=&\left[\begin{array}{ccc}\hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \ r_{1} & r_{2} & r_{3} \ u_{1} & u_{2} & u_{3}\end{array}\right]\
=&(r_{2} u_{3}-r_{3} u_{2}, r_{3} u_{1}-r_{1} u_{3}, r_{1} u_{2}-r_{2} u_{1})
\end{align}
$$
and
$$
\begin{align}
&\mathbf{r} \times \mathbf{v}\
=&\left[\begin{array}{ccc}\hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \ r_{1} & r_{2} & r_{3} \ v_{1} & v_{2} & v_{3}\end{array}\right]\
=&(r_{2} v_{3}-r_{3} v_{2}, r_{3} v_{1}-r_{1} v_{3}, r_{1} v_{2}-r_{2} v_{1}),
\end{align}
$$
so,
$$
\begin{align}
&\mathbf{r} \times(\mathbf{u}+\mathbf{v})\
=&(r_{2} (u_{3}+v_{3})-r_{3} (u_{2}+v_{2}), r_{3} (u_{1}+v_{1})-r_{1} (u_{3}+v_{3}), r_{1} (u_{2}+v_{2})-r_{2} (u_{1}+v_{1}))\
=&(r_{2} u_{3}-r_{3} u_{2}, r_{3} u_{1}-r_{1} u_{3}, r_{1} u_{2}-r_{2} u_{1})\
&+(r_{2} v_{3}-r_{3} v_{2}, r_{3} v_{1}-r_{1} v_{3}, r_{1} v_{2}-r_{2} v_{1})\
=&(\mathbf{r} \times \mathbf{u})+(\mathbf{r} \times \mathbf{v})
\end{align}
$$
this tells us that $\mathbf{r} \times(\mathbf{u}+\mathbf{v})=(\mathbf{r} \times \mathbf{u})+(\mathbf{r} \times \mathbf{v})$, so proved the cross product being distributive.

Proof of (b): We suppose that the $\mathbf{r}$ and $\mathbf{s}$ are vectors that depend on time, mathematically, $\mathbf{r}=\left(r_{1}(t), r_{2}(t), r_{3}(t)\right)$ and $\mathbf{s}=\left(s_{1}(t), s_{2}(t), s_{3}(t)\right)$, we know the cross product would be
$$
\begin{align}
&\mathbf{r} \times \mathbf{s}\
=&\left[\begin{array}{ccc}\hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \ r_{1}(t) & r_{2}(t) & r_{3}(t) \ s_{1}(t) & s_{2}(t) & s_{3}(t)\end{array}\right]\
=&(r_{2}(t) s_{3}(t)-r_{3}(t) s_{2}(t), r_{3}(t) s_{1}(t)-r_{1}(t) s_{3}(t), r_{1}(t) s_{2}(t)-r_{2}(t) s_{1}(t)),
\end{align}
$$
if we take derivative, we would have
$$
\begin{align}
\frac{d}{d t}(\mathbf{r} \times \mathbf{s})
=&(r_{2}(t) s_{3}(t)-r_{3}(t) s_{2}(t), r_{3}(t) s_{1}(t)-r_{1}(t) s_{3}(t), r_{1}(t) s_{2}(t)-r_{2}(t) s_{1}(t))\
=&\left(\frac{d}{d t}r_{2}(t) s_{3}(t)+r_{2}(t) \frac{d}{d t}s_{3}(t)-\frac{d}{d t}r_{3}(t) s_{2}(t)-r_{3}(t) \frac{d}{d t}s_{2}(t)\right.,\
&\frac{d}{d t}r_{3}(t) s_{1}(t)+r_{3}(t) \frac{d}{d t}s_{1}(t)-\frac{d}{d t}r_{1}(t) s_{3}(t)-r_{1}(t) \frac{d}{d t}s_{3}(t),\
&\left.\frac{d}{d t}r_{1}(t) s_{2}(t)+r_{1}(t) \frac{d}{d t}s_{2}(t)-\frac{d}{d t}r_{2}(t) s_{1}(t)-r_{2}(t) \frac{d}{d t}s_{1}(t)\right).
\end{align}
$$
Because of
$$
\begin{align}
&\mathbf{r} \times \frac{d \mathbf{s}}{d t}\
=&\left[\begin{array}{ccc}\hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \ r_{1}(t) & r_{2}(t) & r_{3}(t) \ \frac{d}{d t}s_{1}(t) & \frac{d}{d t}s_{2}(t) & \frac{d}{d t}s_{3}(t)\end{array}\right]\
=&\left(r_{2}(t) \frac{d}{d t}s_{3}(t)-r_{3}(t) \frac{d}{d t}s_{2}(t)\right.,\
&r_{3}(t) \frac{d}{d t}s_{1}(t)-r_{1}(t) \frac{d}{d t}s_{3}(t),\
&\left.r_{1}(t) \frac{d}{d t}s_{2}(t)-r_{2}(t) \frac{d}{d t}s_{1}(t)\right),
\end{align}
$$
and
$$
\begin{align}
&\frac{d \mathbf{r}}{d t} \times \mathbf{s}\
=&\left[\begin{array}{ccc}\hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \ \frac{d}{d t}r_{1}(t) & \frac{d}{d t}r_{2}(t) & \frac{d}{d t}r_{3}(t) \ s_{1}(t) & s_{2}(t) & s_{3}(t)\end{array}\right]\
=&\left(\frac{d}{d t}r_{2}(t) s_{3}(t)-\frac{d}{d t}r_{3}(t) s_{2}(t)\right.,\
&\frac{d}{d t}r_{3}(t) s_{1}(t)-\frac{d}{d t} r_{1}(t) s_{3}(t),\
&\left.\frac{d}{d t} r_{1}(t) s_{2}(t)-\frac{d}{d t} r_{2}(t) s_{1}(t)\right),
\end{align}
$$
hence,
$$
\begin{align}
&\mathbf{r} \times \frac{d \mathbf{s}}{d t}+\frac{d \mathbf{r}}{d t} \times \mathbf{s}\
=&\left(\frac{d}{d t}r_{2}(t) s_{3}(t)+r_{2}(t) \frac{d}{d t}s_{3}(t)-\frac{d}{d t}r_{3}(t) s_{2}(t)-r_{3}(t) \frac{d}{d t}s_{2}(t)\right.,\
&\frac{d}{d t}r_{3}(t) s_{1}(t)+r_{3}(t) \frac{d}{d t}s_{1}(t)-\frac{d}{d t}r_{1}(t) s_{3}(t)-r_{1}(t) \frac{d}{d t}s_{3}(t),\
&\left.\frac{d}{d t}r_{1}(t) s_{2}(t)+r_{1}(t) \frac{d}{d t}s_{2}(t)-\frac{d}{d t}r_{2}(t) s_{1}(t)-r_{2}(t) \frac{d}{d t}s_{1}(t)\right)\
=&\frac{d}{d t}(\mathbf{r} \times \mathbf{s}),
\end{align}
$$
this tells us that $\frac{d}{d t}(\mathbf{r} \times \mathbf{s})=\mathbf{r} \times \frac{d \mathbf{s}}{d t}+\frac{d \mathbf{r}}{d t} \times \mathbf{s}$, so proved the product rule of vector cross product.

John R. Taylor — Question 1.18

Question: The three vectors $\mathbf{a}, \mathbf{b}, \mathbf{c}$ are the three sides of the triangle $A B C$ with angles $\alpha, \beta, \gamma$ as shown in Figure 1.15. (a) Prove that the area of the triangle is given by any one of these three expressions:
$$
\text { area }=\frac{1}{2}|\mathbf{a} \times \mathbf{b}|=\frac{1}{2}|\mathbf{b} \times \mathbf{c}|=\frac{1}{2}|\mathbf{c} \times \mathbf{a}|.
$$
(b) Use the equality of these three expressions to prove the so-called law of sines, thati
$$
\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}.
$$

Proof of (a): Recall for for $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$ and $\mathbf{s}=\left(s_{1}, s_{2}, s_{3}\right)$ with a angle between them $\theta$,
$$|\mathbf{r} \times \mathbf{s}|=|\mathbf{r}| |\mathbf{s}| \sin \theta.$$
We know the area of a triangle is equal to $\frac{1}{2}hl$ for $h$ is the height and $l$ is the corresponding base. Here, we suppose $h$ is the height from point $B$ to base line $\mathbf{b}$. An insight here is to derive $\frac{1}{2}hl$ in from of the three vectors $\mathbf{a}, \mathbf{b}, \mathbf{c}$ with angles $\alpha, \beta, \gamma$, and see if its what we want.

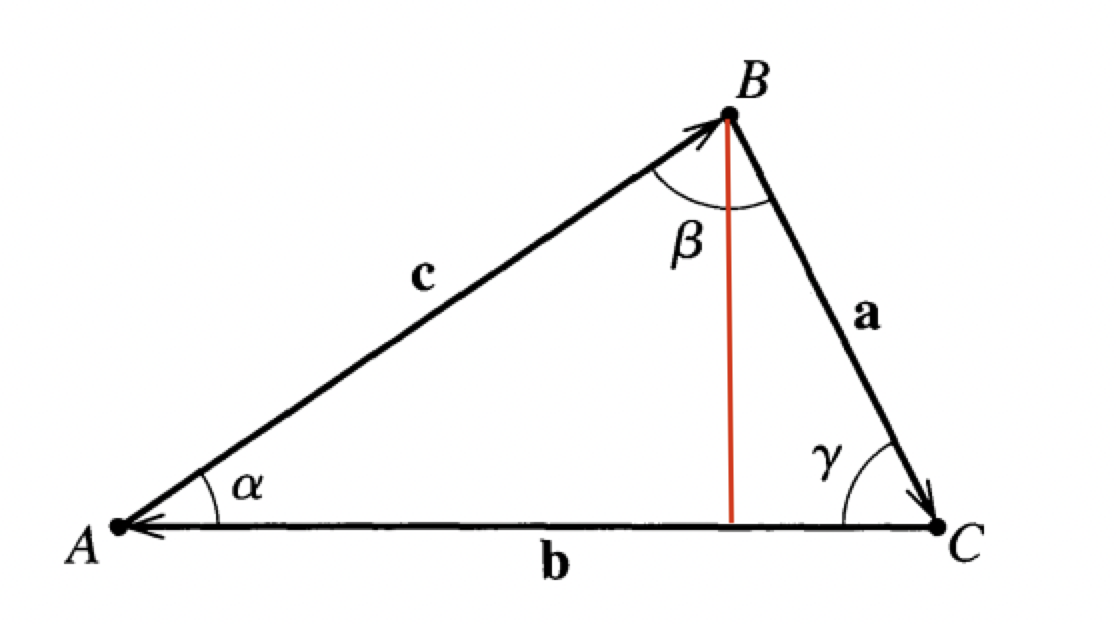
Now, clearly, if $h$ is the height on $\mathbf{b}$, as the red line shown above. Then for the angle $\alpha$, we must have
$$\sin \alpha=\frac{h}{|\mathbf{c}|}\Rightarrow h=\sin \alpha|\mathbf{c}|.$$

Hence then, the base $l$ clearly is the length of vector $\mathbf{b}$ here, so
$$h=|\mathbf{b}|,$$
therefore, because of
$$
\text { area }=\frac{1}{2}hl=\frac{1}{2}|\mathbf{b}|\sin \alpha|\mathbf{c}|=\frac{1}{2}|\mathbf{b}\times\mathbf{c}|.
$$
Similarly, if we take $\mathbf{a}$ as the base, then $h=\sin\gamma|\mathbf{b}|$ and $l=|\mathbf{a}|$, resulting with
$$\text { area }=\frac{1}{2}hl=\frac{1}{2}|\mathbf{a}|\sin\gamma|\mathbf{b}|=\frac{1}{2}|\mathbf{a}\times\mathbf{b}|,$$
and if we take $\mathbf{a}$ as the base, then $h=\sin\beta|\mathbf{a}|$ and $l=|\mathbf{c}|$, resulting with
$$\text { area }=\frac{1}{2}hl=\frac{1}{2}|\mathbf{c}|\sin\beta|\mathbf{a}|=\frac{1}{2}|\mathbf{c}\times\mathbf{a}|.$$
All in all, it is proved that
$$
\text { area }=\frac{1}{2}|\mathbf{a} \times \mathbf{b}|=\frac{1}{2}|\mathbf{b} \times \mathbf{c}|=\frac{1}{2}|\mathbf{c} \times \mathbf{a}|.
$$

Proof of (b): Denote that $|\mathbf{a}|=a$, $|\mathbf{b}|=b$ and $|\mathbf{c}|=c$, because of
$$\frac{1}{2}|\mathbf{a} \times \mathbf{b}|=\frac{1}{2}|\mathbf{b} \times \mathbf{c}|\Longrightarrow |\mathbf{a} \times \mathbf{b}|=|\mathbf{b} \times \mathbf{c}|,$$
we can rewrite it as
$$|\mathbf{a}||\mathbf{b}|\sin\gamma=|\mathbf{b}||\mathbf{c}|\sin\alpha,$$
gives
$$\frac{a}{\sin \alpha}=\frac{c}{\sin \gamma}.$$
Similarly, because of
$$\frac{1}{2}|\mathbf{b} \times \mathbf{c}|=\frac{1}{2}|\mathbf{c} \times \mathbf{a}|\Longrightarrow |\mathbf{b} \times \mathbf{c}|=|\mathbf{c} \times \mathbf{a}|,$$
we can rewrite it as
$$|\mathbf{b}||\mathbf{c}|\sin\alpha=|\mathbf{c}||\mathbf{a}|\sin\beta,$$
gives
$$\frac{b}{\sin \beta}=\frac{a}{\sin \alpha}.$$
Also, because of
$$\frac{1}{2}|\mathbf{a} \times \mathbf{b}|=\frac{1}{2}|\mathbf{c} \times \mathbf{a}|\Longrightarrow |\mathbf{a} \times \mathbf{b}|=|\mathbf{c} \times \mathbf{a}|,$$
we can rewrite it as
$$|\mathbf{a}||\mathbf{b}|\sin\gamma=|\mathbf{c}||\mathbf{a}|\sin\beta,$$
gives
$$\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}.$$
Therefore,
$$
\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}.
$$

John R. Taylor — Question 1.19

Question: If $\mathbf{r}, \mathbf{v}, \mathbf{a}$ denote the position, velocity, and acceleration of a particle, prove that
$$
\frac{d}{d t}[\mathbf{a} \cdot(\mathbf{v} \times \mathbf{r})]=\dot{\mathbf{a}} \cdot(\mathbf{v} \times \mathbf{r}).
$$

Proof: Before actually work on this problem, we recall that for $\mathbf{a},\mathbf{b}$ and $\mathbf{c}$,
$$\mathbf{a} \cdot(\mathbf{b} \times \mathbf{c})=\mathbf{b} \cdot(\mathbf{c} \times \mathbf{a})=\mathbf{c} \cdot(\mathbf{a} \times \mathbf{b})$$
and
$$\frac{d}{d t}(\mathbf{a} \times \mathbf{b})=\frac{d \mathbf{a}}{d t} \times \mathbf{b}+\mathbf{a} \times \frac{d \mathbf{b}}{d t}$$
and
$$\mathbf{a} \times \mathbf{a}=\mathbf{0}.$$
Now start the proof, for $\mathbf{r}$ is the position vector of the particle, the should know that the velocity vector is
$$
\mathbf{v}=\frac{d\mathbf{r}}{dt}=\dot{\mathbf{r}},
$$
and the acceleration vector is
$$
\mathbf{a}=\frac{d\mathbf{v}}{dt}=\frac{d\mathbf{r}^2}{dt^2}=\ddot{\mathbf{r}}.
$$
Therefore,
$$
\begin{align}
\frac{d}{d t}[\mathbf{a} \cdot(\mathbf{v} \times \mathbf{r})]
&=\frac{d}{d t}[\ddot{\mathbf{r}} \cdot(\dot{\mathbf{r}} \times \mathbf{r})]\
&=\frac{d \ddot{\mathbf{r}}}{d t}\cdot \left(\dot{\mathbf{r}} \times \mathbf{r}\right)
+\ddot{\mathbf{r}}\cdot\left(\frac{d \dot{\mathbf{r}}}{d t} \times \mathbf{r}\right)
+\ddot{\mathbf{r}}\cdot\left(\dot{\mathbf{r}} \times \frac{d \mathbf{r}}{d t}\right)\
&=\dddot{\mathbf{r}} \cdot \left(\dot{\mathbf{r}} \times \mathbf{r}\right)
+\ddot{\mathbf{r}}\cdot\left(\ddot{\mathbf{r}} \times \mathbf{r}\right)
+\ddot{\mathbf{r}}\cdot\left(\dot{\mathbf{r}} \times \dot{\mathbf{r}}\right)\
&=\dddot{\mathbf{r}} \cdot \left(\dot{\mathbf{r}} \times \mathbf{r}\right)
+\mathbf{r}\cdot\left(\ddot{\mathbf{r}} \times \ddot{\mathbf{r}}\right)+\mathbf{0}\
&=\dddot{\mathbf{r}} \cdot \left(\dot{\mathbf{r}} \times \mathbf{r}\right)+\mathbf{0}+\mathbf{0}\
&=\dddot{\mathbf{r}} \cdot \left(\dot{\mathbf{r}} \times \mathbf{r}\right)\
&=\dot{\mathbf{a}} \cdot(\mathbf{v} \times \mathbf{r}),
\end{align}
$$
statement proved.

John R. Taylor — Question 1.20

Question: The three vectors $\mathbf{A}, \mathbf{B}, \mathbf{C}$ point from the origin $O$ to the three corners of a triangle. Use the result of Problem $1.18$ to show that the area of the triangle is given by
$$
\text { (area of triangle) }=\frac{1}{2}|(\mathbf{B} \times \mathbf{C})+(\mathbf{C} \times \mathbf{A})+(\mathbf{A} \times \mathbf{B})|.
$$

Answer: The question is shown in the figure, $\mathbf{A}=OA$, $\mathbf{B}=OB$, $\mathbf{C}=OC$. We can see that the whole triangle is divided in three segments. For each of the segments, we know two of its edges in form of vector. Then, we can apply the result from Problem 1.18 above, so
$$\text { area }{\triangle AOB}=\frac{1}{2}|\mathbf{A} \times \mathbf{B}|$$
and
$$\text { area }{\triangle BOC}=\frac{1}{2}|\mathbf{B} \times \mathbf{C}|$$
and
$$\text { area }{\triangle COA}=\frac{1}{2}|\mathbf{C} \times \mathbf{A}|.$$
Therefore, add up all three trangles and it will give us the area of triangle $ABC$:
$$
\begin{align}
\text { area }{\triangle ABC}
&=\text { area }{\triangle AOB}+\text { area }{\triangle BOC}+\text { area }_{\triangle COA}\
&=\frac{1}{2}|\mathbf{A} \times \mathbf{B}|+\frac{1}{2}|\mathbf{B} \times \mathbf{C}|+\frac{1}{2}|\mathbf{C} \times \mathbf{A}|\
&=\frac{1}{2}|(\mathbf{B} \times \mathbf{C})+(\mathbf{C} \times \mathbf{A})+(\mathbf{A} \times \mathbf{B})|.
\end{align}
$$

John R. Taylor — Question 1.22

Question: The two vectors $\mathbf{a}$ and $\mathbf{b}$ lie in the $x y$ plane and make angles $\alpha$ and $\beta$ with the $x$ axis. (a) By evaluating $\mathbf{a} \cdot \mathbf{b}$ in two ways, namely $\mathbf{r} \cdot \mathbf{s}=r s \cos \theta=r_{1} s_{1}+r_{2} s_{2}+r_{3} s_{3}=\sum_{n=1}^{3} r_{n} s_{n},$prove the well-known trig identity
$$
\cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta.
$$
(b) By similarly evaluating $\mathbf{a} \times \mathbf{b}$ prove that
$$
\sin (\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta.
$$

Proof of (a): The Taylor’s book equation (1.6) and (1.7) tells us for $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$ and $\mathbf{s}=\left(s_{1}, s_{2}, s_{3}\right)$,
$$\mathbf{r} \cdot \mathbf{s}=|\mathbf{r}| |\mathbf{s}| \cos \theta.$$
In our case, the difference of $\alpha$ and $\beta$ angle, is exactly the included angle of vectors $\mathbf{a}$ and $\mathbf{b}$, so we can apply the relation above and have
$$\mathbf{a} \cdot \mathbf{b}=|\mathbf{a}| |\mathbf{b}| \cos \theta=|\mathbf{a}| |\mathbf{b}| \cos (\alpha-\beta),$$
remember, the vectors can be expressed by Pythagorean theorem, that is,
$$
\begin{align}
\mathbf{a}&=(a_1,a_2,0)=(|\mathbf{a}| \cos \alpha,|\mathbf{a}| \sin \alpha,0)=|\mathbf{a}|(\cos \alpha,\sin \alpha,0)\
\mathbf{b}&=(b_1,b_2,0)=(|\mathbf{b}| \cos \beta,|\mathbf{b}| \sin \beta,0)=|\mathbf{b}|(\cos \beta,\sin \beta,0),
\end{align}
$$
so easily get
$$
\begin{align}
\mathbf{a} \cdot \mathbf{b}
&=|\mathbf{a}| |\mathbf{b}| \cos \alpha \cos \beta+|\mathbf{a}| |\mathbf{b}| \sin \alpha \sin \beta\
&=|\mathbf{a}| |\mathbf{b}|(\cos \alpha \cos \beta+\sin \alpha \sin \beta)
=|\mathbf{a}| |\mathbf{b}| \cos (\alpha-\beta),\ \
&\Rightarrow \cos \alpha \cos \beta+\sin \alpha \sin \beta=\cos (\alpha-\beta).
\end{align}
$$

Part (a) is proved, it is true for trig identity $\cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta$.

Proof of (b): A similar formula that works for the corss product is the following, still for $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$ and $\mathbf{s}=\left(s_{1}, s_{2}, s_{3}\right)$ with a angle between them $\theta$,
$$|\mathbf{r} \times \mathbf{s}|=|\mathbf{r}| |\mathbf{s}| \sin \theta.$$
In our case, apply the relation above and have
$$|\mathbf{a} \times \mathbf{b}|=|\mathbf{a}| |\mathbf{b}| \sin \theta=|\mathbf{a}| |\mathbf{b}| \sin (\alpha-\beta),$$
exactly the same, expressed the vectors with help of the Pythagorean theorem, so,
$$
\begin{align}
\mathbf{a}&=(a_1,a_2,0)=(|\mathbf{a}| \cos \alpha,|\mathbf{a}| \sin \alpha,0)\
\mathbf{b}&=(b_1,b_2,0)=(|\mathbf{b}| \cos \beta,|\mathbf{b}| \sin \beta,0),
\end{align}
$$
the last part is quite different
$$
\begin{align}
|\mathbf{a} \times \mathbf{b}|
&=\left|\operatorname{det}\left[\begin{array}{ccc}\hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \ |\mathbf{a}| \cos \alpha & |\mathbf{a}| \sin \alpha & 0 \ |\mathbf{b}| \cos \beta & |\mathbf{b}| \sin \beta & 0\end{array}\right]\right|\
&=\sqrt{(0)^2+(0)^2+(|\mathbf{a}| \cos \alpha |\mathbf{b}| \sin \beta-|\mathbf{a}| \sin \alpha |\mathbf{b}| \cos \beta)^2}\
&=|\mathbf{a}| \sin \alpha |\mathbf{b}| \cos \beta-|\mathbf{a}| \cos \alpha |\mathbf{b}| \sin \beta\
&=|\mathbf{a}| |\mathbf{b}|(\sin \alpha \cos \beta - \cos \alpha \sin \beta)
=|\mathbf{a}| |\mathbf{b}| \sin (\alpha-\beta),\ \
&\Rightarrow \sin \alpha \cos \beta - \cos \alpha \sin \beta=\sin (\alpha-\beta).
\end{align}
$$

Part (b) is proved, it is true for trig identity $\sin (\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta$.

John R. Taylor — Question 1.23

Question: The unknown vector $\mathbf{v}$ satisfies $\mathbf{b} \cdot \mathbf{v}=\lambda$ and $\mathbf{b} \times \mathbf{v}=\mathbf{c}$, where $\lambda, \mathbf{b}$, and $\mathbf{c}$ are fixed and known. Find $\mathbf{v}$ in terms of $\lambda, \mathbf{b}$, and $\mathbf{c}$.

Answer: We know that, for any vector $\mathbf{r}=\left(r_{1}, r_{2}, r_{3}\right)$, there must be $r=|\mathbf{r}|=\sqrt{\mathbf{r} \cdot \mathbf{r}}$.

For the equation $\mathbf{b} \cdot \mathbf{v}=\lambda$, we have
$$
\mathbf{v}(\mathbf{b} \cdot \mathbf{b})=\mathbf{v} |\mathbf{b}|^{2}
\Rightarrow
\mathbf{v}(\mathbf{b} \cdot \mathbf{b})+\mathbf{b}(\mathbf{b} \cdot \mathbf{v})-\mathbf{b}(\mathbf{b} \cdot \mathbf{v})=\mathbf{v} |\mathbf{b}|^{2},
$$
then, because of the distributive property $\mathbf{a} \times(\mathbf{b} \times \mathbf{c})=\mathbf{b}(\mathbf{a} \cdot \mathbf{c})-\mathbf{c}(\mathbf{a} \cdot \mathbf{b})$,
$$
\begin{align}
\mathbf{v}(\mathbf{b} \cdot \mathbf{b})+\mathbf{b}(\mathbf{b} \cdot \mathbf{v})-\mathbf{b}(\mathbf{b} \cdot \mathbf{v})
&=\mathbf{b}(\mathbf{b} \cdot \mathbf{v})-\mathbf{b}(\mathbf{b} \cdot \mathbf{v})+\mathbf{v}(\mathbf{b} \cdot \mathbf{b})\
&=\mathbf{b}(\mathbf{b} \cdot \mathbf{v})-[\mathbf{b}(\mathbf{b} \cdot \mathbf{v})-\mathbf{v}(\mathbf{b} \cdot \mathbf{b})]\
&=\mathbf{b}(\mathbf{b} \cdot \mathbf{v})-\mathbf{b} \times(\mathbf{b} \times \mathbf{v}),
\end{align}
$$
because of satisfing $\mathbf{b} \cdot \mathbf{v}=\lambda$ and $\mathbf{b} \times \mathbf{v}=\mathbf{c}$,
$$
\begin{align}
\mathbf{v}(\mathbf{b} \cdot \mathbf{b})+\mathbf{b}(\mathbf{b} \cdot \mathbf{v})-\mathbf{b}(\mathbf{b} \cdot \mathbf{v})
&=\mathbf{b}(\mathbf{b} \cdot \mathbf{v})-\mathbf{b} \times(\mathbf{b} \times \mathbf{v})\
&=\mathbf{b}(\lambda)-\mathbf{b} \times(\mathbf{c})\
&=\mathbf{v} |\mathbf{b}|^{2}.
\end{align}
$$
so that
$$
\mathbf{v}=\frac{\lambda\mathbf{b}-\mathbf{b} \times\mathbf{c}}{|\mathbf{b}|^{2}}.
$$
This is the vector $\mathbf{v}$ we have found.